 Flat-Earth Folly by Dave Matson
Flat-Earth Folly by Dave Matson We are as gods compared to the ancients. The ingenious Greeks actually deduced the spherical shape and size of the Earth. But they never dreamed that a day would arrive when astronauts would routinely see the curvature of the Earth, when satellites would photograph the whole sphere of the Earth time and time again, when mechanical probes from a variety of nations would actually visit those "wandering stars" that are spherical planets, and it would have blown their minds to have known that men would actually stand on the moon and gaze upon a very spherical Earth.
In this age of wonders there is an odd, little society in the United States that fancies that the Earth is flat. Not surprisingly, religion is behind it. A spherical Earth just doesn't fit in with their flat-earth book known as the Bible. But, give them some credit. At least they realize that the Bible is a flat-earth book. Unfortunately, they resolved that annoying conflict with reality by throwing out reality itself! In doing so they have advanced the cause of humor over the years by being the butt of numerous jokes.
In a flat-earther's world of deep denial, all of the wonders above turn into giant hoaxes or conspiracies! Never mind that even president Nixon's inner circle couldn't keep a secret for long or that Hoover's FBI couldn't keep its dirtiest secrets safe! We are asked to believe that whole nations, with their ever-changing governments, that hundreds of eminent scientists and corporations are part of a perfectly orchestrated conspiracy! Moreover, this conspiracy is so incredibly perfect in juggling its infinitely many operations (from phony factories, phony space centers complete with phony launches, phony scientific papers, phony reports from phony weather satellites, and the ability to recruit legions of people who will never spill the beans) that even decades later it remains totally credible, the best efforts of debunkers notwithstanding! Anyone who can swallow that whale is clearly at the deepest level of denial and well beyond the reach of reason and evidence. In the real world such a conspiracy--if it could ever be put together--would immediately explode at a thousand different points. After all these years such a conspiracy would have been trampled like grass under a herd of elephants! The need to believe in such a vast, flawless conspiracy is enough reason to reject the flat-earth claim. However, I will add two more arguments for the record.
My first argument is as basic as gravity itself. On a scale the size of the moon, let alone Earth, gravity completely overpowers the cohesiveness of rock. Given its great mass, which can easily be calculated in any modern physics laboratory, the only shape the Earth can have is a spherical one. For the same reason, we observe that all the planets in our solar system, as well as their larger moons, are spherical. For that same reason, our sun is spherical. Careful measurements may reveal slight deviations due to rotation and other factors, but for all practical purposes we're talking about spheres.
My second argument rests squarely on the certainty of mathematics. It immediately settles the issue and no other arguments need be considered.
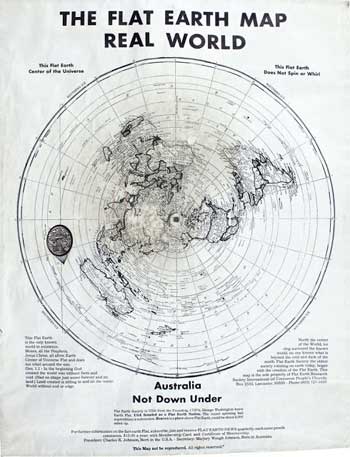
Mathematicians have proven that there is no way to convert an accurate spherical map to an accurate flat map. Neither can you convert an accurate flat map into an accurate spherical map. If you have any doubts, try a couple of experiments. First, set the intact rind of half an orange onto a flat sheet. You will quickly discover that it must be ripped in numerous places in order to flatten it. Many points (think of little "cities") that were initially next to each other on the rind are now clearly separated. That is to say, the flattened version of the orange hemisphere distorts any map on it. (I used half of an intact rind because it is easy to scoop out the pulp. I can't even imagine flattening a whole rind into a single sheet without massive ripping!
Going the other way, try fitting a sheet of paper onto a tennis ball. You can't avoid getting all kinds of wrinkles or folds, meaning that if you began with the same amount of sheet area as the tennis ball you would not have enough to cover that tennis ball! Moreover, many points (think of little "cities") that are clearly separated from one another on the flat sheet will now be next to one another as the intervening space got folded up. Clearly, a flat map cannot be translated into a faithful spherical map.
If you want a mathematical approach, consider any triangular space on a rotating sphere defined by a point at the north pole and two points on the equator, the latter being arranged so that all distances between these three points are equal. We will make this sphere 8000 miles in diameter so that the results will be comparable to the earthly situation. Thus, each of our three points would be separated by about 6280 miles from each other. If we considered no other measurements, we could come up with a flat map that gave those distances. It would be an equilateral triangle with sides 6280 miles long.
Now, on our spherical map, consider the midpoint within our first three points, the midpoint being equally far from each of those points. Do the math (using the distance formula, a bit of trig, and an elementary use of vectors) and you will find that this midpoint is about 3820 miles from each of the first three points. Understand that on a spherical map distance is measured along the surface.
Now, calculate the middle point to the equilateral triangle on our flat map. You will find that the distance between it and any of the other three points is about 3623 miles! Thus, that distance is nearly 200 miles shorter on the flat map than on the spherical map. Since there is only one midpoint in either case, it becomes clear that a spherical map cannot accurately translate to a flat map. The reverse is also true. If you begin with a reasonably-sized equilateral triangle on a flat map, a little more math will make it clear that there is no such triangle on the sphere that has the right lengths for its sides and the correct distance between its midpoint and the other three. The discrepancy will be obvious. That leads us to our grand conclusion.
Whoever produces an accurate map wins the debate! Moreover, the accuracy need only be eyeball good since, if one side has a reasonable map, the other side must have a map that is manifestly off in places. We're not talking about itty-bitty differences that might be explained away by some subtlety! We will have a clear winner unless Earth has another shape altogether! A nice feature of this test is that, if an accurate spherical map is presented, we don't even have to look at flat-earth maps since no accurate flat-earth map could possibly exist. And, vice versa. This conclusion has the stamp of mathematical certainty.
Take a globe that is at least 8 inches in diameter (better accuracy) and use string and painter's blue masking tape (less sticky, won't hurt your globe) to get the distances between 10 major cities or ports, and convert those string distances to a scaled-up globe of 8000 miles diameter. Make sure those cities are spread out over an area (rather than in a line) in order to get a proper test. Compare your results to any number of accepted tables that give the distances between these cities. You will find that your globe gives a remarkably good fit. Therefore, no accurate flat-earth map exists. And, no flat-earth exists since it would surely allow an accurate flat-earth map.
The flat-earther is nailed to the cross in that his only escape is to argue that nobody really knows the distances between the major cities and ports. Such a claim would have been absurd even in the last days of sail! In the Age of GPS, where the distances between cities can be measured with an accuracy of less than an inch, such a claim becomes hysterically ludicrous! We "round-earthers" have the map; We win!
Dave E. Matson

